Project Overview
This project was part of the Machine Learning for Time Series course by Laurent Oudre. Together with Guillaume Levy, I reimplemented two papers on symbolic representations of time series, focusing on the ABBA method (Adaptive Brownian Bridge-based symbolic Aggregation).
Our objectives were to understand how ABBA compresses and encodes time series and evaluate whether ABBA representations can be combined with LSTMs for forecasting, compared to raw time series baselines.
Why symbolic representations?
Time series often pose challenges for deep learning: they are long, noisy, and contain redundant patterns. Symbolic representations like ABBA attempt to compress a signal into a sequence of discrete symbols, preserving its key dynamics while reducing dimensionality.
Potential benefits include:
- Lower computational cost for training and inference
- Improved interpretability of recurring patterns
- A bridge between symbolic analysis and modern deep learning models
The ABBA method
ABBA converts a time series into symbols through three main stages:
-
Segmentation: The signal is approximated with piecewise linear segments. Segments are chosen adaptively to respect a maximum reconstruction error.
-
Quantization / Symbolization: Segment slopes and lengths are clustered (e.g., with k-means), and each cluster is mapped to a symbol. This builds a discrete dictionary of patterns.
-
Reconstruction – From the sequence of symbols, an approximate version of the original time series can be reconstructed, enabling lossy compression.
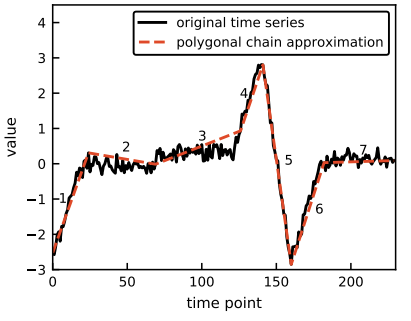
The promise is that instead of modeling thousands of raw values, one can train models on much shorter symbolic sequences.
More details on the method can be found in the report.
Experiments
We tested ABBA on two datasets: Synthetic sinusoidal signal (clean, periodic) and Monthly Sunspots dataset (real-world, noisy, quasi-periodic).
Reconstruction quality
- On the sinusoidal dataset, ABBA reconstructs the signal almost perfectly.
- On the Sunspots dataset, more symbols are required to capture variability, and reconstruction is less precise.
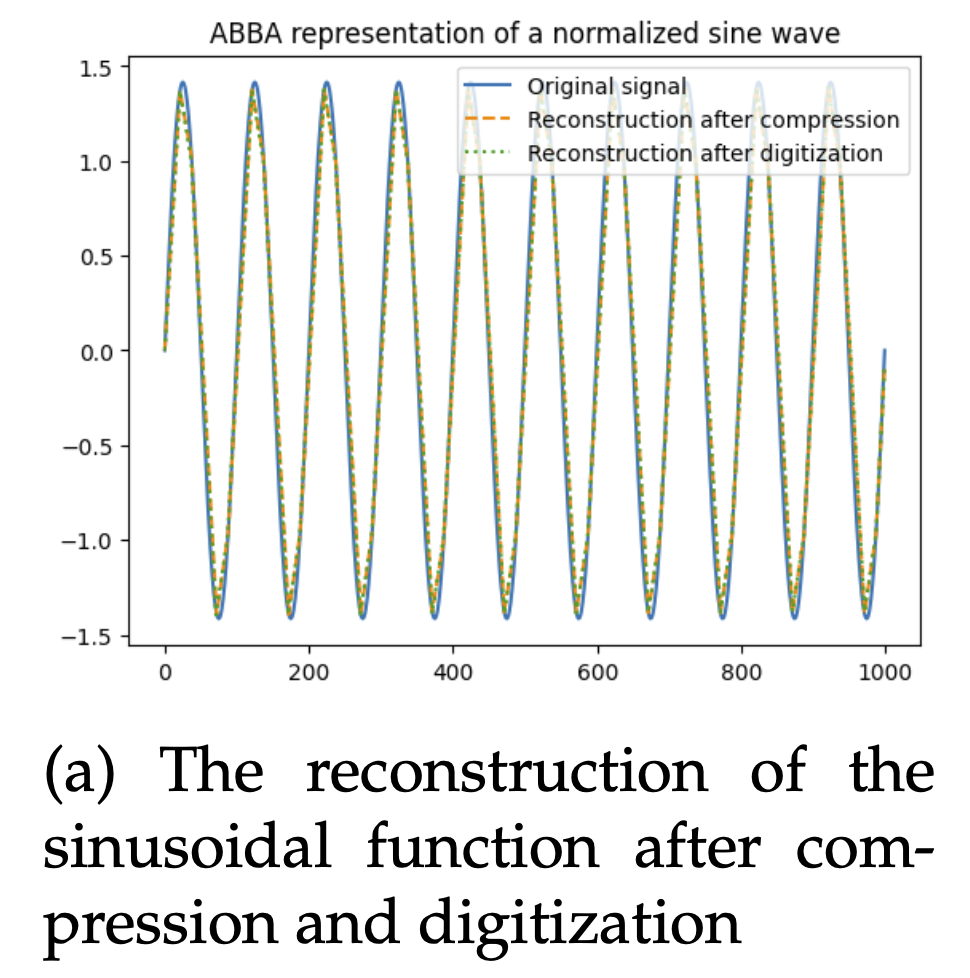
ABBA reconstruction on a sinusoidal dataset
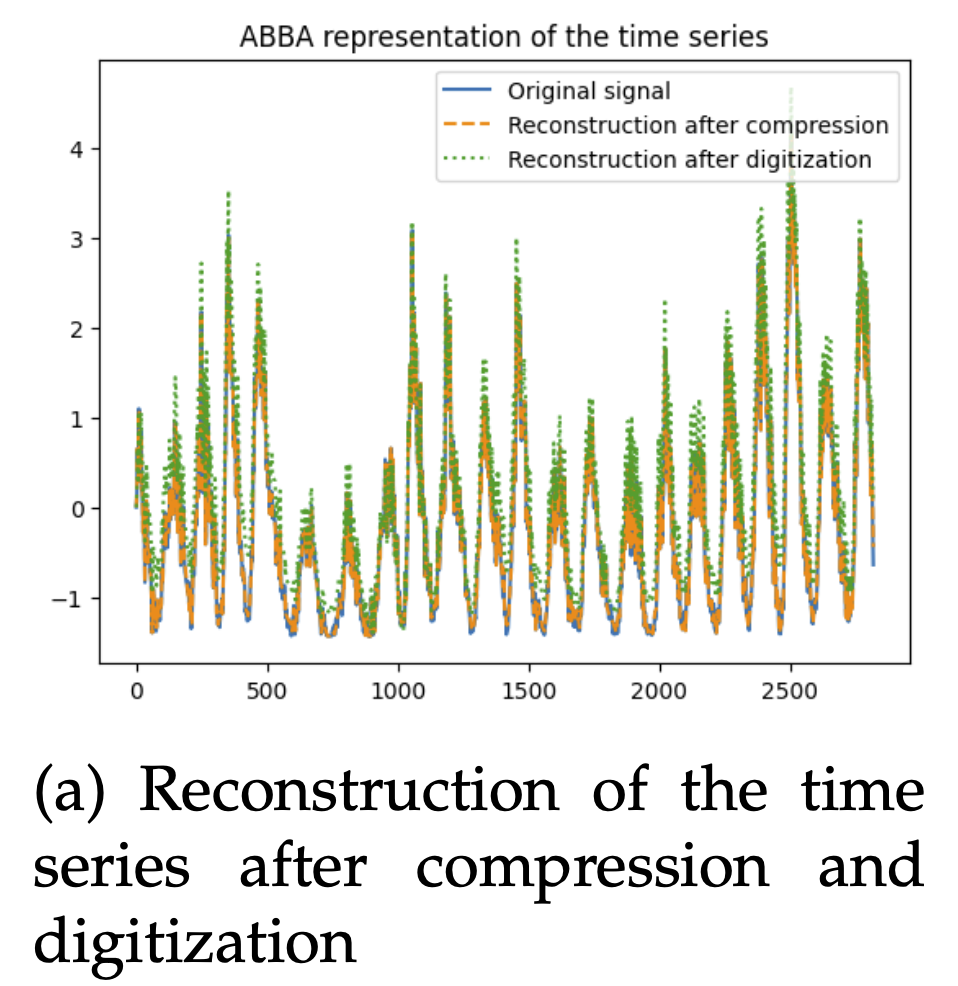
ABBA reconstruction on the Sunspots dataset
While reconstruction is decent, one can already question whether symbol sequences without inherent numerical meaning are suitable inputs for forecasting.
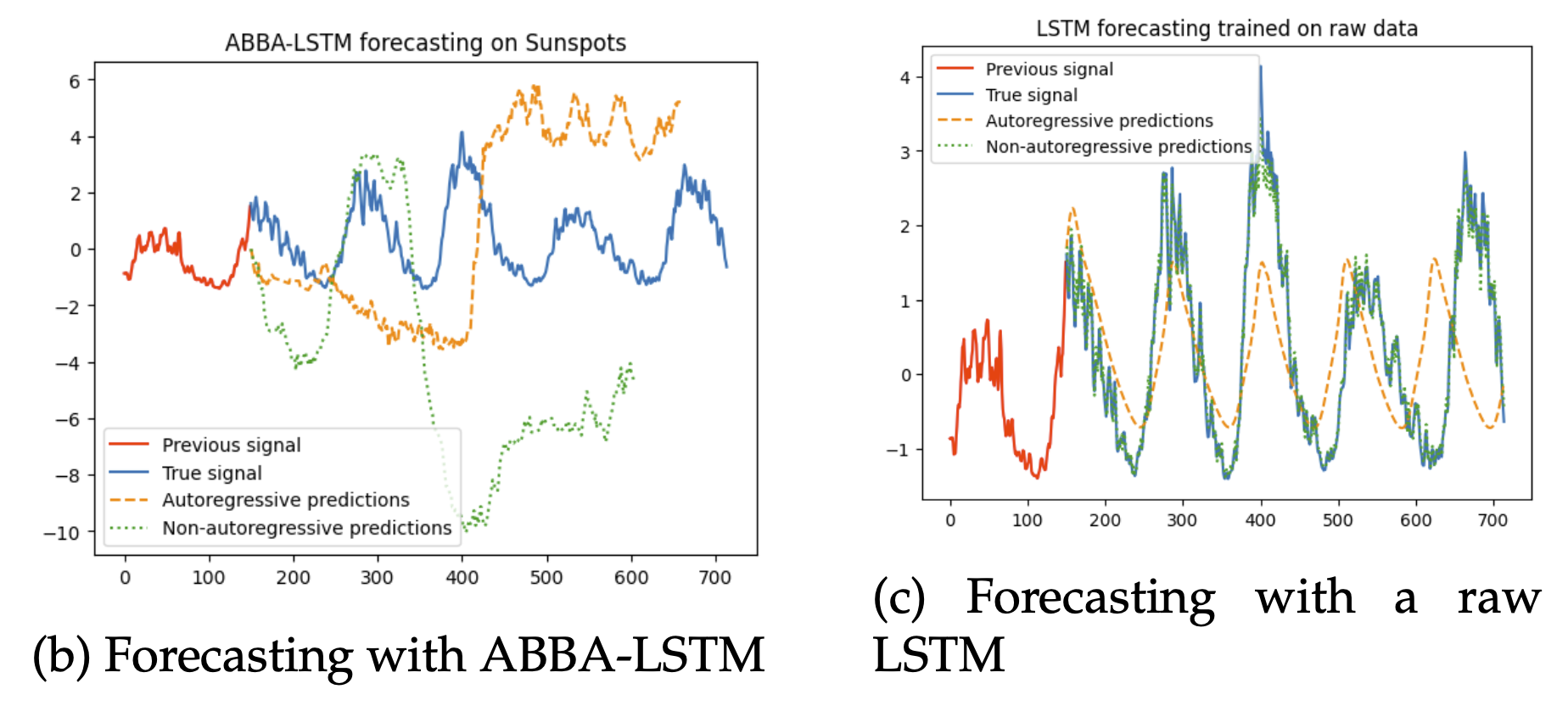
Forecasting with LSTM
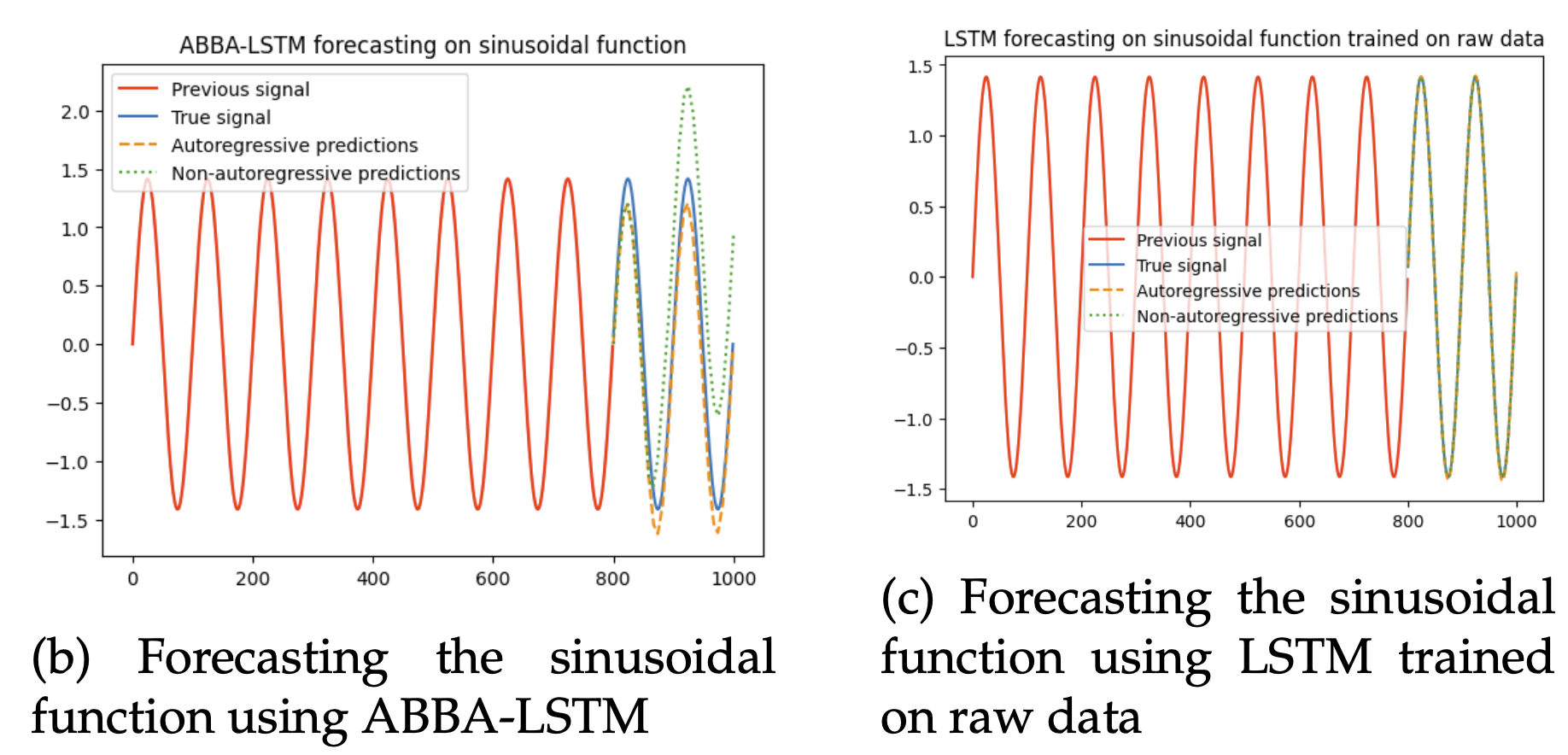
We compared two forecasting approaches: Raw LSTM trained directly on raw time series values and ABBA-LSTM trained on ABBA-generated symbol sequences.
| Dataset | Raw LSTM (DTW ↓) | ABBA-LSTM (DTW ↓) |
|---|---|---|
| Sinusoidal | 0.001–0.015 | 0.034–0.134 |
| Sunspots | 0.022–0.068 | 0.319–0.357 |
Across both datasets, ABBA-LSTM performed significantly worse. This outcome is unsurprising: ABBA compresses signals into a symbolic dictionary, but those symbols carry no semantic or numerical continuity for forecasting models.
Critical findings
Initially, we were surprised at the discrepancy between our results and those reported in the original papers. After reviewing the authors’ official implementation, we discovered some methodological inconsistencies between the paper and the code. More importantly, the paper reported results where models were trained directly on the test set, inflating performance.
This was extremely disappointing, especially given the publication venue (Data Mining and Knowledge Discovery). It was a valuable lesson in the importance of looking at both code and methodology when reproducing research.
Documentation
References
- Elsworth, S., & Güttel, S. (2020). ABBA: Adaptive Brownian bridge-based symbolic aggregation of time series. Data Mining and Knowledge Discovery, 34(4), 1175-1200. Link
- Elsworth, S., & Güttel, S. (2020). Time series forecasting using LSTM networks: A symbolic approach. arXiv preprint arXiv:2003.05672. Link