Project Overview
This project was part of the Theoretical Principles of Deep Learning course taught by Hedi Hadiji.
Together with Guillaume Levy, I reimplemented the experiments of the paper:
Arora, S., Cohen, N., & Hazan, E. (2018). On the Optimization of Deep Networks: Implicit Acceleration by Overparameterization. Proceedings of ICML 2018. arXiv:1802.06509
The paper shows that increasing the depth of a neural network, with linear layers without activations, can accelerate training. This effect is not due to added expressiveness (since stacked linear layers are equivalent to a single one), but rather emerges from how optimization dynamics change when the network is overparameterized.
Theoretical Background
Consider a network of depth N with only linear layers and no activations. In function space, this is equivalent to a single linear transformation.
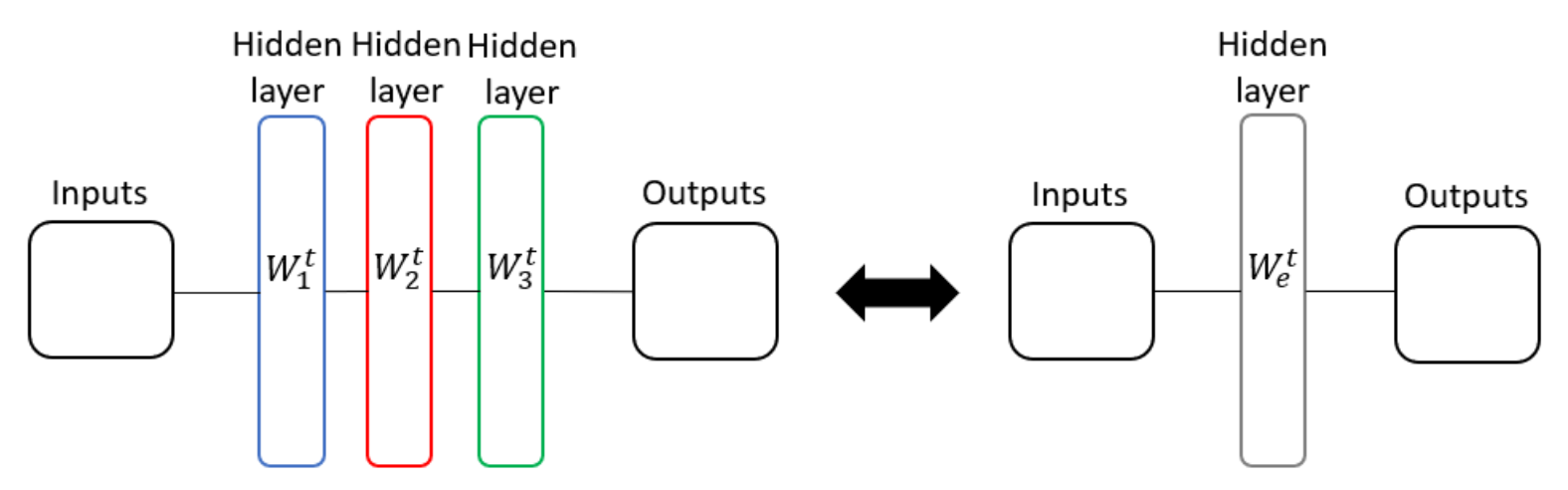
Despite functional equivalence, the optimization trajectory differs. When training each layer with SGD, the equivalent one-layer model effectively inherits an adaptive learning rate depending on weight norms and a form of implicit momentum that comes from how gradients propagate through layers.
These properties are not introduced by hand (like with Adam or momentum SGD), but arise naturally from depth. This is why the phenomenon is called implicit acceleration. This is a counterintuitive result, as it suggests that adding more layers without activations can actually improve training.
See the full proof in the report.
Experiments
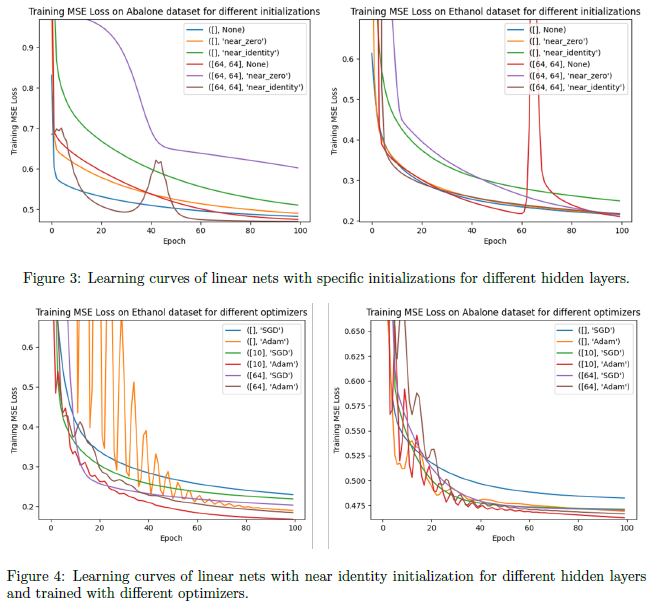
To test these ideas, we trained networks with 1, 2, and 3 linear layers on two datasets: the Gas Sensor Array Dataset for ethanol concentration prediction and the Abalone Dataset for predicting age from physical features.
Our experimental setup included a grid search over learning rates to isolate convergence effects, comparison of different initializations (near-zero vs. near-identity matrices), and comparison with other optimizers such as Adam.
Observations
Results were highly dependent on initialization and dataset. In some cases, deeper linear networks converged faster (supporting the theory), while in others, a simple one-layer model or Adam optimizer outperformed. Overparameterization occasionally introduced instability in the form of “bursts” in training loss.
Final Thoughts
While the math suggests a universal implicit acceleration effect, in practice the results depend heavily on initialization, optimizer choice, and dataset. The key insight is that depth does not only affect expressiveness of neural networks, it also changes the optimization landscape in subtle ways.
Our experiments did not align with the paper’s results. Since the paper was published at ICML, we would have expected the results to be accurate and consistant. Looking at other projects from the course, it seemed that it was pretty common that results differed from the papers. Since the paper is rather simple, I do not think that our experiments were wrong. It made me wonder how much we can trust the results of papers.