Project Overview
As part of the Reinforcement Learning course by Stergios Christodoulidis, I implemented reinforcement learning algorithms to train an agent to play Text Flappy Bird (TFB), a simplified version of the classic game. The environment is defined by a compact state space describing the bird’s vertical position and distance to the next pipe.
The challenge was to design agents that could learn to survive as long as possible knowing where the next pipe is.
Algorithms
The state space is a 2D vector (height, distance to next pipe).
I experimented with two classical RL approaches:
Monte Carlo Control (MCC)
Monte Carlo Control learns action-value functions by averaging returns observed over complete episodes. After generating trajectories of states, actions, and rewards, the algorithm updates policies to maximize long-term rewards. While intuitive, MCC requires full episodes for updates, which can make training slow and unstable.
Sarsa(λ)
Sarsa(λ) combines temporal difference learning with eligibility traces, enabling continuous updates at each time step. The λ parameter controls how much past transitions influence learning. Compared to MCC, Sarsa(λ) is more stable and convenient to train since it does not rely on full episodes.
Both methods used a decaying epsilon-greedy exploration strategy: the agent explores randomly at the start and gradually shifts toward exploitation of the learned policy.
Results
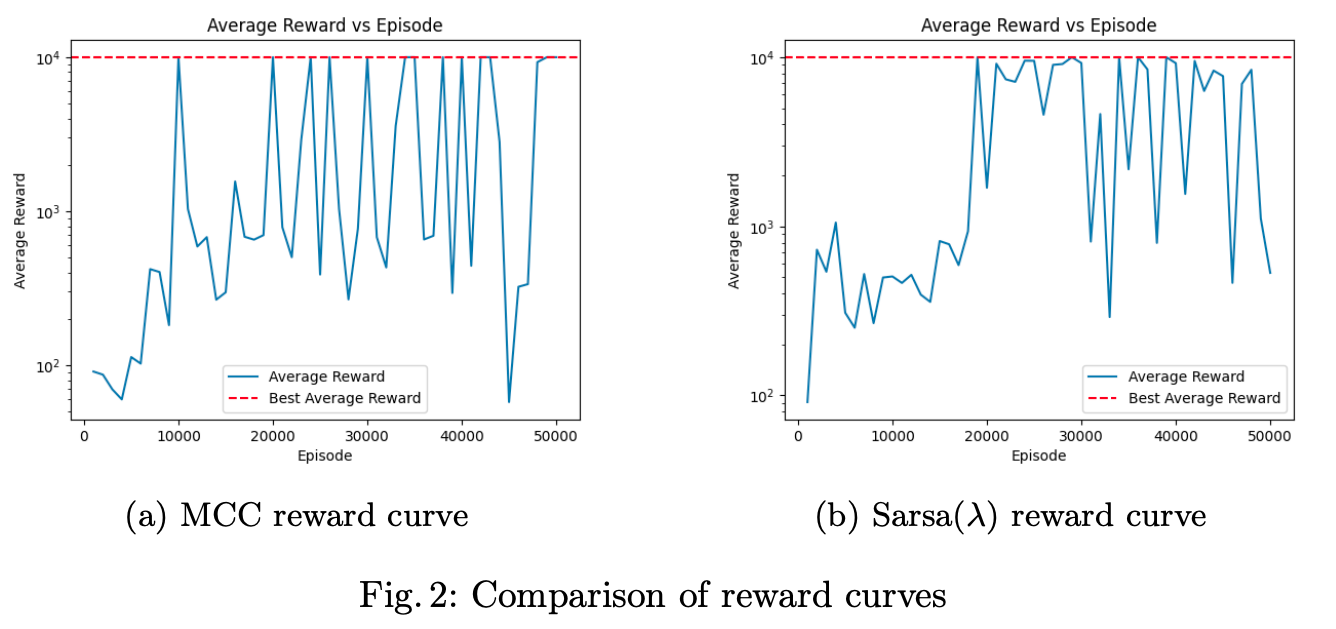
Both MCC and Sarsa(λ) converged to nearly optimal policies. The learned agents successfully flapped when necessary and remained idle otherwise, achieving high rewards compared to hand-crafted baselines such as always-flap or greedy heuristics.
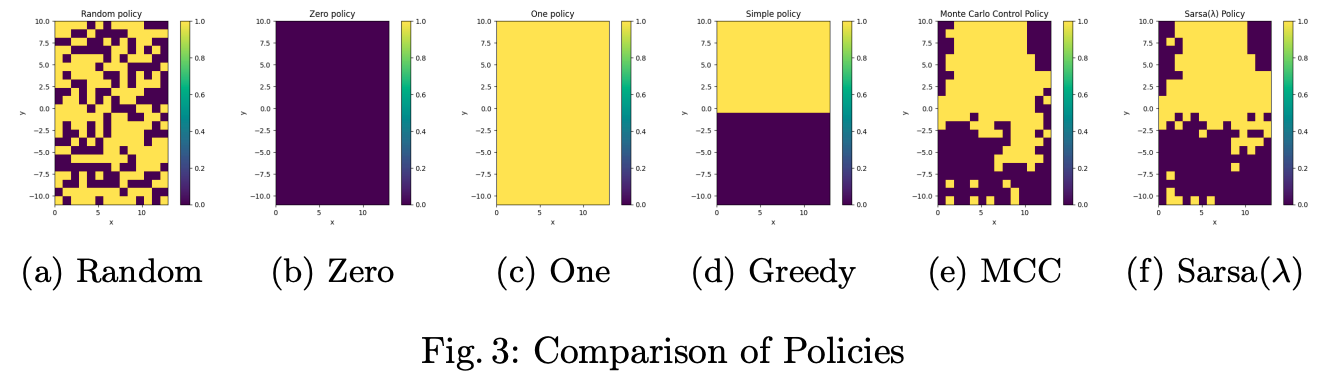
Interestingly, the MCC converged slightly faster but showed instability while Sarsa(λ) was more robust and provided stable convergence.
Possible extensions
- From TFB to Original Flappy Bird: Extending to the full game requires extracting visual features of the next pipe position. This suggests moving from tabular methods to Deep Q-Learning (DQN) with convolutional encoders.
- Generalization to New Configurations: Agents trained on one configuration (pipe gap, grid size) struggled to generalize to unseen ones. Smaller gaps and taller grids required retraining, showing limits of tabular RL without richer representations.
