Project Overview
This project was carried out as part of the Machine Learning on Network Science course taught by Fragkiskos Malliaros.
Our goal was to benchmark several Graph Neural Network (GNN) architectures on the Twitch Gamers dataset, a large-scale social network of streamers.
Previous studies mainly relied on classical node embeddings, designed to preserve proximity or structural roles. Here, we explore how modern GNNs perform on a range of supervised learning tasks, both classification and regression.
We focused on four predictive tasks:
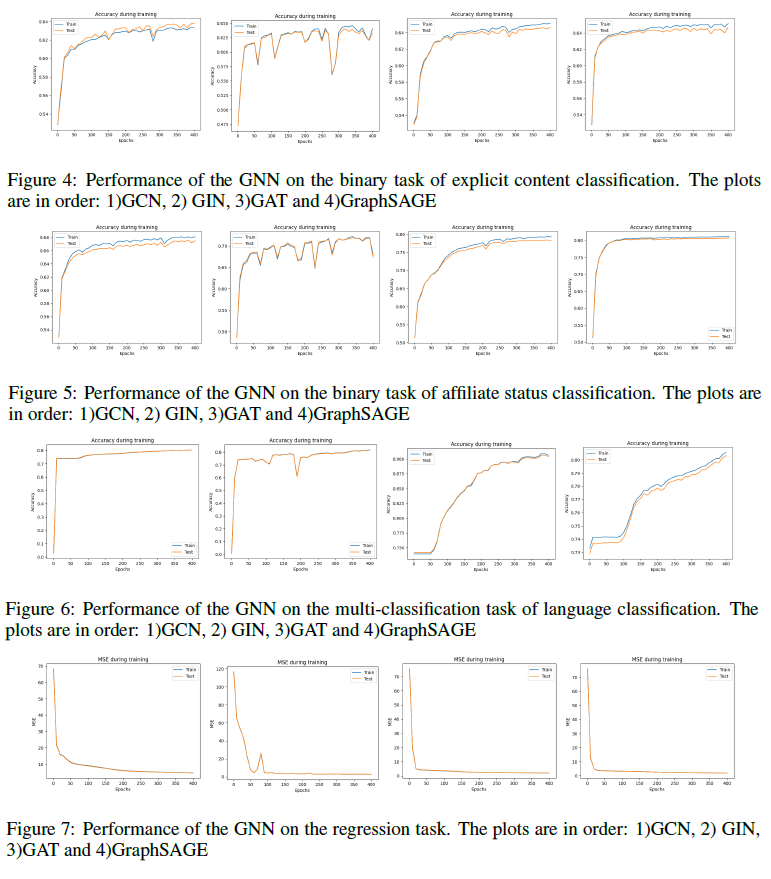
- Detecting channels with explicit content
- Predicting affiliate status
- Classifying broadcast languages
- Regressing the number of views
To this end, we compared four widely used GNN architectures: Graph Convolutional Network (GCN), Graph Isomorphism Network (GIN), Graph Attention Network (GAT), and GraphSAGE.
Dataset
The Twitch Gamers dataset (Rozemberczki et al., 2018) contains 168k streamers (nodes) and 6.79M mutual friendships (edges). Each node comes with rich metadata, including:
- Language (one per streamer)
- Affiliate status (binary)
- Explicit content flag (binary)
- Creation and last activity dates
- Account activity (alive vs dead)
- Number of views
- Account lifetime (days between first and last stream)
The graph is a single connected component, undirected, and label-complete. However, the distribution of labels is highly skewed: for example, English dominates the language attribute, which makes naïve baselines surprisingly strong.
Formally, we denote the graph as:
\[G = (V, E), \quad |V| = 168k, \; |E| = 6.79M\]with node features $X \in \mathbb{R}^{\vert V \vert \times d}$ and adjacency matrix $A \in \{0,1\}^{\vert V \vert \times \vert V \vert}$.
Learning Tasks
We frame the four tasks as node-level prediction problems. For each node $v_i \in V$, we aim to learn a function:
\[f: (X, A) \mapsto Y\]where $Y$ is the label set. Depending on the task:
- Binary classification: explicit content, affiliate status
- Multi-class classification: broadcast language
- Regression: viewer count
The models are trained using standard objectives:
- Classification (cross-entropy loss):
- Regression (mean squared error):
Methods
We compare four GNN architectures, each with a different way of propagating information across the graph.
Graph Convolutional Network (GCN)
GCNs generalize CNNs to graphs by aggregating features from immediate neighbors with normalization by node degrees.
\[X' = \hat{D}^{-1/2} \hat{A} \hat{D}^{-1/2} X \Theta\]where $\hat{A} = A + I$ includes self-loops, and $\hat{D}$ is its degree matrix.
Graph Isomorphism Network (GIN)
GINs are designed to be as expressive as the Weisfeiler-Lehman isomorphism test. They aggregate neighbor features with a learnable scaling:
\[X' = \text{MLP}\left((1+\epsilon) X + \sum_{j \in \mathcal{N}(i)} X_j\right)\]where $\epsilon$ is either fixed or learnable.
Graph Attention Network (GAT)
GATs assign different weights to neighbors using an attention mechanism:
\[x'_i = \sigma\!\left(\sum_{j \in \mathcal{N}(i)} \alpha_{ij} \, W x_j \right), \quad \alpha_{ij} = \frac{\exp(\text{LeakyReLU}(a^\top [Wx_i \| Wx_j]))}{\sum_{k \in \mathcal{N}(i)} \exp(\text{LeakyReLU}(a^\top [Wx_i \| Wx_k]))}\]where $|$ denotes concatenation.
GraphSAGE
GraphSAGE enables inductive learning by sampling and aggregating neighborhood information:
\[x'_i = \sigma\!\left(W \cdot \text{AGG}\left(\{x_j, \; j \in \mathcal{N}(i)\}\right) \; \| \; W' x_i\right)\]where AGG can be mean, max-pool, or LSTM.
Results & Discussion
While none of the models solved the tasks perfectly, our benchmark highlights how different architectures specialize in different aspects of the data. Future work could integrate more recent GNN variants (e.g., Graph Transformers, scalable spectral methods).
Documentation
-
Previous
Flappy Bird Reinforcement Learning -
Next
NLP: Emotion Classification with Aspect-Based Sentiment Analysis
