Accelerating Nash Equilibrium Convergence with Google DeepMind

Project Overview

During my final year at CentraleSupélec, I had the opportunity to collaborate with Google DeepMind on a research project (Oct 2023 – Apr 2024) focused on improving the convergence of algorithms for computing Nash equilibria in two-player zero-sum games.

Finding Nash equilibria is a central objective in game theory. The FoReL framework offers strong theoretical guarantees and scales to very large games (e.g., Stratego with \(10^{535}\) states, compared to chess with \(10^{123}\) states). Yet, to tackle even more complex domains, we need to accelerate FoReL’s convergence. Our project targeted exactly this challenge.

We propose Population Alternating Lyapunov FoReL (PAL-FoReL): an algorithm that marries FoReL’s theoretical strengths with population-based ideas. In normal-form games (Matching Pennies, Rock-Paper-Scissors, Kuhn Poker), our experiments demonstrate orders-of-magnitude faster convergence than existing methods.

For full details, see the technical report.

Background

This section provides a concise overview of normal-form games, Nash equilibria, and the FoReL algorithm. It includes the essential concepts needed to understand the method and results.

Normal-Form Games (NFG)

A normal-form game is defined by: \((\Pi, u, K)\)

\(\Pi = (\Pi^1, \dots, \Pi^K)\): the strategy sets for each player
\(u: \Pi \to \mathbb{R}^K\): the payoff function
\(K\): the number of players

Each player \(k\) selects a (possibly mixed) strategy \(\pi^k\), forming a strategy profile \(\pi = (\pi^1, \dots, \pi^K)\). The expected utility for player \(k\) is: \(\overline{u}^k(\pi) = \mathbb{E}_{a \sim \pi}[u^k(a)].\)

Example: In Rock-Paper-Scissors, \(\pi^1\) is a probability distribution over \(\{R,P,S\}\) (similarly for \(\pi^2\)). Once both players pick their mixed strategies, they together define the profile \(\pi = (\pi^1, \pi^2)\), from which we compute expected utilities. For instance, a player might mix 50% Rock and 50% Paper, hence the need for expectations.

Nash Equilibrium

A best response for player \(k\) is: \(BR^k(\pi^{-k}) = \arg\max_{\pi^k} \overline{u}^k(\pi^k, \pi^{-k}).\)

Intuitively, this is the strategy for player \(k\) that maximizes expected utility given the others’ strategies.

A Nash equilibrium \(\pi^*\) satisfies: \(\pi^{k*} = BR^k(\pi^{-k*}), \quad \forall k.\)

At equilibrium, no player can benefit by unilaterally deviating. Nash equilibria may not be unique, but they exist under standard conditions.

To quantify proximity to equilibrium, we use NashConv:

\[\text{NashConv}(\pi) = \sum_k \left[ \overline{u}^k(BR^k(\pi^{-k}), \pi^{-k}) - \overline{u}^k(\pi) \right].\]

\(\text{NashConv} = 0\): the profile is at equilibrium
Larger values indicate greater deviation from equilibrium

NashConv is a practical convergence metric computable even without explicit knowledge of the equilibrium.

Deriving FoReL

We briefly introduce the key ideas behind FoReL (Follow-the-Regularized-Leader).

For a trajectory of mixed strategies \(x(t)\), the regret for player \(k\) is: \(Reg_k(\tilde{t}) = \max_{p_k \in \chi_k} \left\{ \frac{1}{\tilde{t}} \int_0^{\tilde{t}} \Big[u_k\big(p_k; x_{-k}(s)\big) - u_k\big(x(s)\big)\Big] \, ds \right\}.\)

Intuition: \(Reg_k(\tilde{t})\) measures how much better player \(k\) could have done, on average, by always playing the best fixed strategy. A player has no regret if: \(\limsup_{t \to \infty} Reg_k(t) \leq 0.\)

FoReL updates are defined by:

\[y_k(t) = \int_0^t \overline{u}^k(\pi(s)) \, ds,\quad \pi^k(t) = \arg\max_{\pi^k \in \chi_k} \big( \langle y_k(t), \pi^k \rangle - H(\pi^k) \big),\]

where \(H\) is an entropy regularizer that encourages exploration by smoothing policies. With entropy regularization, FoReL reduces to Replicator Dynamics:

\[\frac{d}{dt} \pi^k(a) = \pi^k(a) \left[ u(a, \pi) - \overline{u}^k(\pi) \right].\]

Intuition: Actions performing above the current policy value are reinforced and played more frequently.

While vanilla FoReL is no-regret, its trajectories are Poincaré recurrent: they orbit around equilibria without converging. For instance, in RPS, pure best-responses lead to perpetual cycling (Rock → Paper → Scissors → Rock → …).

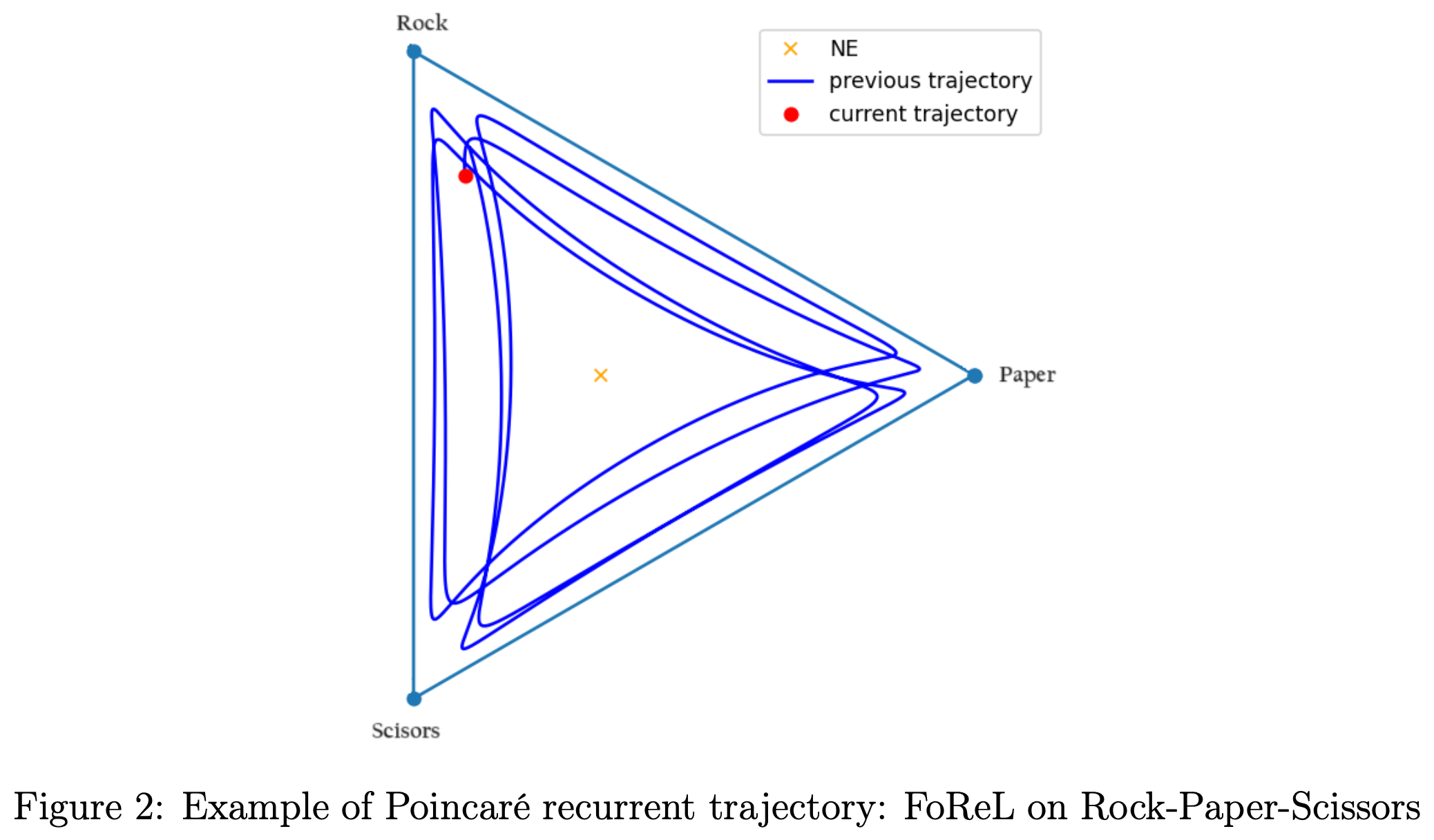
Poincaré recurrence in Rock-Paper-Scissors

Reward Transformation

Viewing the dynamics through the lens of trajectories and energy, we can add a “friction” term to encourage convergence. This is achieved by making rewards policy-dependent:

\[R_{\pi}^k(a^k, a^{-k}) = r^k(a^k, a^{-k}) - \eta \log \left( \frac{\pi^k(a^k)}{\mu^k(a^k)} \right) + \eta \log \left( \frac{\pi^{-k}(a^{-k})}{\mu^{-k}(a^{-k})} \right).\]

With this reward transformation, trajectories converge to the equilibrium of the modified game. As \(\eta \to 0\), the equilibrium approaches that of the original game. This idea is called Decaying Lyapunov FoReL (DL-FoReL). However, in practice DL-FoReL can converge poorly: locally shrinking \(\eta\) removes the reason of the convergence.

To improve this, Perolat et al. (2021) proposed iteratively setting the friction anchor as: \(\mu = \pi_t,\) leading to Iterative Lyapunov FoReL (IL-FoReL), which exhibits much better convergence than DL-FoReL.

DL-FoReL and IL-FoReL on Matching Pennies

Our objective is to design a method that converges even faster than IL-FoReL.

Method: Extending FoReL

Our core idea is to combine Lyapunov FoReL with a population of policies to better approximate the Nash equilibrium.

We introduce two methods:

An oracle-inspired variant, L*-FoReL, which uses the true equilibrium as the Lyapunov anchor (for diagnosis and upper-bound analysis).
Two practical methods that approximate the anchor via populations: Pop-FoReL and PAL-FoReL.

L*-FoReL

Consider FoReL with reward transformation. What is the optimal choice of \(\mu\)? Since \(\mu\) acts as a friction anchor encouraging trajectories to stay near it, the optimal choice is the Nash equilibrium \(\pi^*\). Empirically, using: \(\mu = \pi^*\) yields faster convergence than IL-FoReL. We call this method L*-FoReL.

Of course, \(\pi^*\) is unknown in practice, so L*-FoReL is not a usable algorithm. However, it provides a valuable upper bound on achievable convergence rates and highlights a large room for improvement between IL-FoReL and the L*-FoReL ideal.

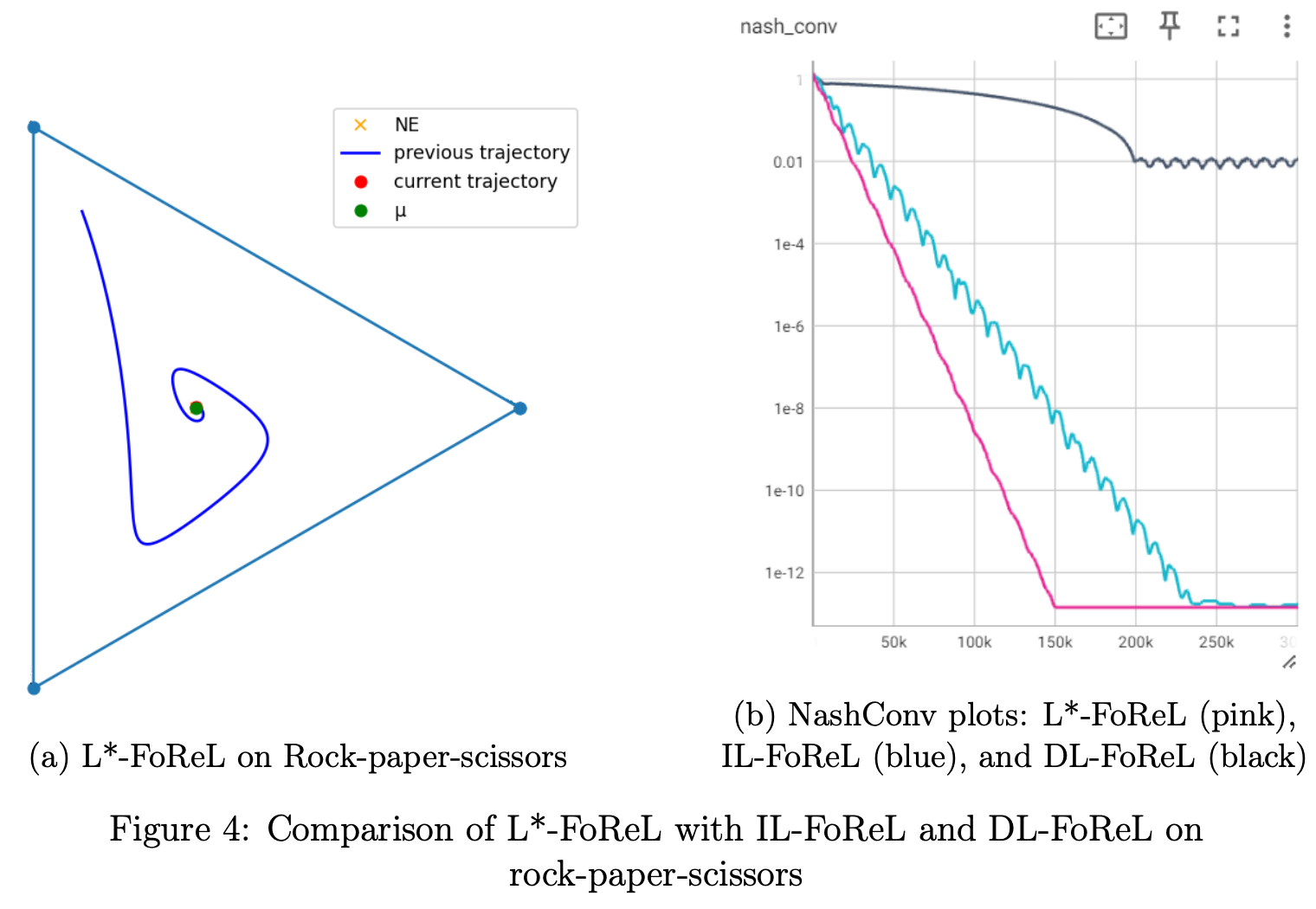
L*-FoReL on Rock-Paper-Scissors

Pop-FoReL and PAL-FoReL

Because L*-FoReL is impractical, we need to approximate \(\pi^*\). A classical insight is that time-averaging Vanilla FoReL iterates converges to equilibrium. We leverage this in two ways:

1) Population FoReL (Pop-FoReL): Maintain a population of vanilla FoReL policies and periodically average them to form a new iterate. This empirically verifies that averaging drives convergence. While averaging tabular policies is straightforward, averaging neural policies can be nontrivial in large games.

2) Population Alternating Lyapunov FoReL (PAL-FoReL): Use population averaging to build the Lyapunov anchor \(\mu\), then alternate between:

Exploration: Vanilla FoReL steps (diversify and collect good policies)
Exploitation: Reward-Transformed FoReL steps with the current \(\mu\) (stabilize and accelerate convergence)

A key advantage: even when policies are represented by neural networks, we only need inference to evaluate the reward transformation with \(\mu\), making PAL-FoReL practical.

Algorithm: Population FoReL (Pop-FoReL)

Inputs:
- n_iteration: number of outer iterations
- n_steps_PC: number of vanilla FoReL steps per iteration
- sample_and_average_population: procedure to sample and average the population

Initialize:
- Population P ← ∅
- Policy π ← initial policy

For iteration = 1 to n_iteration:
  For step = 1 to n_steps_PC:
    π ← FoReL_iteration(π)
    Add π to population P
  π ← sample_and_average_population(P)
  Reset population P ← ∅

Return final π

Algorithm: Population Alternating Lyapunov FoReL (PAL-FoReL)

Inputs:
- n_iteration: number of outer iterations
- n_steps_PC: number of vanilla FoReL steps per iteration (Exploration)
- n_steps_L: number of Lyapunov steps per iteration (Exploitation)
- sample_and_average_population: procedure to sample and average the population
- η: Lyapunov/regularization strength

Initialize:
- Population P ← ∅
- Policy π ← initial policy
- Anchor μ ← π

For iteration = 1 to n_iteration:
  # Exploration phase (vanilla FoReL)
  For pc_step = 1 to n_steps_PC:
    π ← FoReL_iteration(π)
    Add π to population P

  # Build Lyapunov anchor from population
  μ ← sample_and_average_population(P)
  Reset population P ← ∅

  # Exploitation phase (Lyapunov FoReL with anchor μ)
  For l_step = 1 to n_steps_L:
    π ← Lyapunov_FoReL_iteration(π, η, μ)

Return final π

Results on Kuhn Poker

Kuhn Poker is a two-player imperfect-information game with a 3-card deck (1, 2, 3). Despite its small size, it presents key challenges for equilibrium computation. We validate our methods on Kuhn Poker and find that PAL-FoReL and Pop-FoReL converge several orders of magnitude faster than IL-FoReL, both in:

Model-based settings (exact payoff function known), and
Model-free settings (payoff approximated via Monte Carlo estimates).

FoReL on Kuhn Poker

We also explored a range of hyperparameters (e.g., population size, number of steps per phase, anchor update cadence) and sampling/averaging schemes. Additional details are provided in the project report.

Documentation

📄 Complete Project Report
💻 GitHub Repository

References

Mertikopoulos, Papadimitriou, Piliouras. Cycles in Adversarial Regularized Learning. SODA, 2018.
Perolat et al. From Poincaré Recurrence to Convergence in Imperfect Information Games. ICML, 2021.
Perolat et al. Mastering Stratego with Model-Free Multi-Agent Reinforcement Learning. Science, 2022.
Hennes et al. Neural Replicator Dynamics. arXiv:1906.00190, 2019.

Accelerating Nash Equilibrium Convergence with Google DeepMind ⭐ ⭐

Population-Based Enhancements for Faster FoReL Convergence